For at beregne området for en trekant skal du kende dens højde. For at finde højden følg disse instruktioner. Du skal i det mindste have en base for at finde højden.
Metode En af tre:
Brug af base og område for at finde højde
-
 1 Husk formlen for området af en trekant. Formlen for området af en trekant er A = 1 / 2BH. [1]
1 Husk formlen for området af en trekant. Formlen for området af en trekant er A = 1 / 2BH. [1] - EN = Triangelens område
- b = Længden af bunden af trekanten
- h = Højde af bunden af trekanten
-
 2 Se på din trekant og bestem hvilke variabler du kender. Du kender allerede området, så tildel værdien til EN. Du bør også kende værdien af en sidelængde; tildele denne værdi til "'b'". Enhver side af en trekant kan være bunden, uanset hvordan trekanten trækkes. For at visualisere dette, kan du forestille dig at rotere trekanten, indtil den kendte sidelængde er i bunden. Eksempel
2 Se på din trekant og bestem hvilke variabler du kender. Du kender allerede området, så tildel værdien til EN. Du bør også kende værdien af en sidelængde; tildele denne værdi til "'b'". Enhver side af en trekant kan være bunden, uanset hvordan trekanten trækkes. For at visualisere dette, kan du forestille dig at rotere trekanten, indtil den kendte sidelængde er i bunden. Eksempel
Hvis du ved, at arealet af en trekant er 20, og den ene side er 4, så:
A = 20 og b = 4.
-
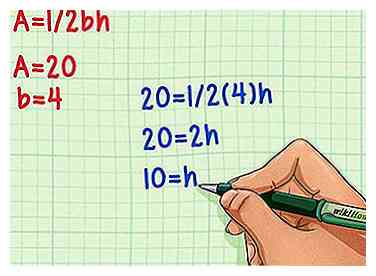 3 Slut dine værdier til ligningen A = 1 / 2BH og gør matematikken. Først multipliceres basen (b) med 1/2, divider derefter området (A) af produktet. Den resulterende værdi bliver højden på din trekant! Eksempel
3 Slut dine værdier til ligningen A = 1 / 2BH og gør matematikken. Først multipliceres basen (b) med 1/2, divider derefter området (A) af produktet. Den resulterende værdi bliver højden på din trekant! Eksempel
20 = 1/2 (4) h Indsæt tallene i ligningen.
20 = 2 timer Multiplicer 4 ved 1/2.
10 = h Opdel med 2 for at finde værdien for højden.
Metode To af tre:
Finde en lige sidelængdehøjde
-
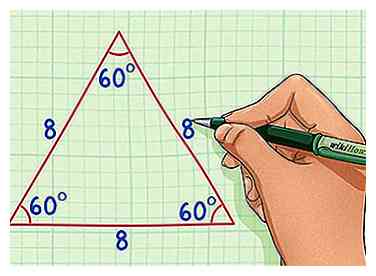 1 Husk egenskaberne af en ligesidet trekant. En ligesidet trekant har tre lige sider og tre lige vinkler, der hver er 60 grader. Hvis du skærer en ligesidet trekant i halvdelen, vil du ende med to kongruente højre trekanter. [2]
1 Husk egenskaberne af en ligesidet trekant. En ligesidet trekant har tre lige sider og tre lige vinkler, der hver er 60 grader. Hvis du skærer en ligesidet trekant i halvdelen, vil du ende med to kongruente højre trekanter. [2] - I dette eksempel bruger vi en ligesidet trekant med sidelængder på 8.
-
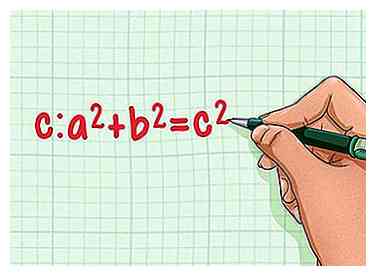 2 Husk den pythagoriske sætning. Pythagoras sætning siger for enhver ret trekant med sider af længden -en og b, og hypotenuse af længde c: -en2 + b2 = c2. Vi kan bruge denne sætning til at finde højden af vores ligesidede trekant![3]
2 Husk den pythagoriske sætning. Pythagoras sætning siger for enhver ret trekant med sider af længden -en og b, og hypotenuse af længde c: -en2 + b2 = c2. Vi kan bruge denne sætning til at finde højden af vores ligesidede trekant![3] -
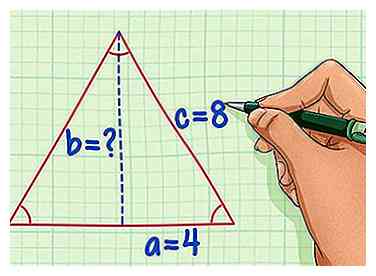 3 Bryd den ligesidede trekant i halvdelen, og tildel værdier til variabler -en, b, og c. Den hypotese c vil være lig med den oprindelige sidelængde. Side -en vil være lig med 1/2 sidelængde og side b er højden af trekanten, som vi skal løse.
3 Bryd den ligesidede trekant i halvdelen, og tildel værdier til variabler -en, b, og c. Den hypotese c vil være lig med den oprindelige sidelængde. Side -en vil være lig med 1/2 sidelængde og side b er højden af trekanten, som vi skal løse. - Ved hjælp af vores eksempel ligesidede trekant med sider på 8, c = 8 og a = 4.
-
 4 Indsæt værdierne i Pythagoras sætning og løs for b2. Første plads c og -en ved at gange hvert nummer af sig selv. Træk derefter a2 fra c2. Eksempel
4 Indsæt værdierne i Pythagoras sætning og løs for b2. Første plads c og -en ved at gange hvert nummer af sig selv. Træk derefter a2 fra c2. Eksempel
42 + b2 = 82 Indsæt værdierne for a og c.
16 + b2 = 64 Firkant a og c.
b2 = 48 Træk en2 fra c2.
-
 5 Find kvadratroden af b2 for at få højden af din trekant! Brug kvadratrodsfunktionen på din regnemaskine for at finde Sqrt (2. Svaret er højden af din ligesidede trekant!
5 Find kvadratroden af b2 for at få højden af din trekant! Brug kvadratrodsfunktionen på din regnemaskine for at finde Sqrt (2. Svaret er højden af din ligesidede trekant! - b = Sqrt (48) = 6.93
Metode Tre af tre:
Bestemmelse af højde med vinkler og sider
-
 1 Bestem hvilke variabler du kender. Højden på en trekant kan findes, hvis du har 2 sider og vinklen mellem dem eller alle tre sider. Vi kalder siderne af trekanten a, b og c, og vinklerne A, B og C.
1 Bestem hvilke variabler du kender. Højden på en trekant kan findes, hvis du har 2 sider og vinklen mellem dem eller alle tre sider. Vi kalder siderne af trekanten a, b og c, og vinklerne A, B og C. - Hvis du har alle tre sider, vil du bruge Herons formel, og formlen for området af en trekant.
- Hvis du har to sider og en vinkel, vil du bruge formlen for området givet to vinkler og en side. A = 1 / 2ab (sin C).[4]
-
 2 Brug Herons formel, hvis du har alle tre sider. Herons formel har to dele. For det første skal du finde variablen s, som er lig med halvdelen af omkredsen af trekanten. Dette gøres ved hjælp af denne formel: s = (a + b + c) / 2.[5] Herons formeleksempel
2 Brug Herons formel, hvis du har alle tre sider. Herons formel har to dele. For det første skal du finde variablen s, som er lig med halvdelen af omkredsen af trekanten. Dette gøres ved hjælp af denne formel: s = (a + b + c) / 2.[5] Herons formeleksempel
For en trekant med sider a = 4, b = 3 og c = 5:
s = (4 + 3 + 5) / 2
s = (12) / 2
s = 6
Brug derefter den anden del af Herons formel, Område = sqr (s (s-a) (s-b) (s-c). Erstat område i ligningen med dets ækvivalent i området formel: 1 / 2bh (eller 1 / 2ah eller 1 / 2ch).
Løs for h. For vores eksempel trekant ser det ud som:
1/2 (3) h = sqr (6 (6-4) (6-3) (6-5).
3 / 2h = sqr (6 (2) (3) (1)
3 / 2h = sqr (36)
Brug en regnemaskine til at beregne kvadratroden, hvilket i dette tilfælde gør det 3 / 2h = 6.
Derfor er højden lig med 4, ved hjælp af side b som basis.
-
 3 Brug området givet to sider og en vinkelformel, hvis du har en side og en vinkel. Erstat område i formlen med dets ækvivalent i området med en trekant formel: 1 / 2bh. Dette giver dig en formel, der ligner 1 / 2bh = 1 / 2ab (sin C). Dette kan forenkles til h = a (sin C), hvorved en af sidevariablerne elimineres.[6] Find højde med 1 side og 1 vinkel eksempel
3 Brug området givet to sider og en vinkelformel, hvis du har en side og en vinkel. Erstat område i formlen med dets ækvivalent i området med en trekant formel: 1 / 2bh. Dette giver dig en formel, der ligner 1 / 2bh = 1 / 2ab (sin C). Dette kan forenkles til h = a (sin C), hvorved en af sidevariablerne elimineres.[6] Find højde med 1 side og 1 vinkel eksempel
For eksempel, med a = 3 og C = 40 grader, ser ligningen sådan ud:
h = 3 (sin 40)
Brug din regnemaskine til at afslutte ligningen, hvilket gør h ca. 1.928.
 Minotauromaquia
Minotauromaquia
 1 Husk formlen for området af en trekant. Formlen for området af en trekant er A = 1 / 2BH. [1]
1 Husk formlen for området af en trekant. Formlen for området af en trekant er A = 1 / 2BH. [1]  2 Se på din trekant og bestem hvilke variabler du kender. Du kender allerede området, så tildel værdien til EN. Du bør også kende værdien af en sidelængde; tildele denne værdi til "'b'". Enhver side af en trekant kan være bunden, uanset hvordan trekanten trækkes. For at visualisere dette, kan du forestille dig at rotere trekanten, indtil den kendte sidelængde er i bunden.
2 Se på din trekant og bestem hvilke variabler du kender. Du kender allerede området, så tildel værdien til EN. Du bør også kende værdien af en sidelængde; tildele denne værdi til "'b'". Enhver side af en trekant kan være bunden, uanset hvordan trekanten trækkes. For at visualisere dette, kan du forestille dig at rotere trekanten, indtil den kendte sidelængde er i bunden. 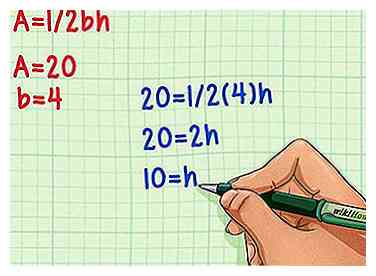 3 Slut dine værdier til ligningen A = 1 / 2BH og gør matematikken. Først multipliceres basen (b) med 1/2, divider derefter området (A) af produktet. Den resulterende værdi bliver højden på din trekant!
3 Slut dine værdier til ligningen A = 1 / 2BH og gør matematikken. Først multipliceres basen (b) med 1/2, divider derefter området (A) af produktet. Den resulterende værdi bliver højden på din trekant!  1 Husk egenskaberne af en ligesidet trekant. En ligesidet trekant har tre lige sider og tre lige vinkler, der hver er 60 grader. Hvis du skærer en ligesidet trekant i halvdelen, vil du ende med to kongruente højre trekanter. [2]
1 Husk egenskaberne af en ligesidet trekant. En ligesidet trekant har tre lige sider og tre lige vinkler, der hver er 60 grader. Hvis du skærer en ligesidet trekant i halvdelen, vil du ende med to kongruente højre trekanter. [2] 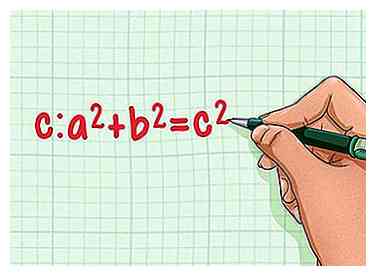 2 Husk den pythagoriske sætning. Pythagoras sætning siger for enhver ret trekant med sider af længden -en og b, og hypotenuse af længde c: -en2 + b2 = c2. Vi kan bruge denne sætning til at finde højden af vores ligesidede trekant![3]
2 Husk den pythagoriske sætning. Pythagoras sætning siger for enhver ret trekant med sider af længden -en og b, og hypotenuse af længde c: -en2 + b2 = c2. Vi kan bruge denne sætning til at finde højden af vores ligesidede trekant![3]  3 Bryd den ligesidede trekant i halvdelen, og tildel værdier til variabler -en, b, og c. Den hypotese c vil være lig med den oprindelige sidelængde. Side -en vil være lig med 1/2 sidelængde og side b er højden af trekanten, som vi skal løse.
3 Bryd den ligesidede trekant i halvdelen, og tildel værdier til variabler -en, b, og c. Den hypotese c vil være lig med den oprindelige sidelængde. Side -en vil være lig med 1/2 sidelængde og side b er højden af trekanten, som vi skal løse.  4 Indsæt værdierne i Pythagoras sætning og løs for b2. Første plads c og -en ved at gange hvert nummer af sig selv. Træk derefter a2 fra c2.
4 Indsæt værdierne i Pythagoras sætning og løs for b2. Første plads c og -en ved at gange hvert nummer af sig selv. Træk derefter a2 fra c2.  5 Find kvadratroden af b2 for at få højden af din trekant! Brug kvadratrodsfunktionen på din regnemaskine for at finde Sqrt (2. Svaret er højden af din ligesidede trekant!
5 Find kvadratroden af b2 for at få højden af din trekant! Brug kvadratrodsfunktionen på din regnemaskine for at finde Sqrt (2. Svaret er højden af din ligesidede trekant!  1 Bestem hvilke variabler du kender. Højden på en trekant kan findes, hvis du har 2 sider og vinklen mellem dem eller alle tre sider. Vi kalder siderne af trekanten a, b og c, og vinklerne A, B og C.
1 Bestem hvilke variabler du kender. Højden på en trekant kan findes, hvis du har 2 sider og vinklen mellem dem eller alle tre sider. Vi kalder siderne af trekanten a, b og c, og vinklerne A, B og C.  2 Brug Herons formel, hvis du har alle tre sider. Herons formel har to dele. For det første skal du finde variablen s, som er lig med halvdelen af omkredsen af trekanten. Dette gøres ved hjælp af denne formel: s = (a + b + c) / 2.[5]
2 Brug Herons formel, hvis du har alle tre sider. Herons formel har to dele. For det første skal du finde variablen s, som er lig med halvdelen af omkredsen af trekanten. Dette gøres ved hjælp af denne formel: s = (a + b + c) / 2.[5]  3 Brug området givet to sider og en vinkelformel, hvis du har en side og en vinkel. Erstat område i formlen med dets ækvivalent i området med en trekant formel: 1 / 2bh. Dette giver dig en formel, der ligner 1 / 2bh = 1 / 2ab (sin C). Dette kan forenkles til h = a (sin C), hvorved en af sidevariablerne elimineres.[6]
3 Brug området givet to sider og en vinkelformel, hvis du har en side og en vinkel. Erstat område i formlen med dets ækvivalent i området med en trekant formel: 1 / 2bh. Dette giver dig en formel, der ligner 1 / 2bh = 1 / 2ab (sin C). Dette kan forenkles til h = a (sin C), hvorved en af sidevariablerne elimineres.[6]