At finde den tredje vinkel på en trekant, når du kender målingerne af de to andre vinkler er let. Alt du skal gøre er at trække de andre vinkelmålinger fra 180 ° for at få måling af den tredje vinkel. Der er dog et par andre måder at finde måling af den tredje vinkel på en trekant på, afhængigt af det problem, du arbejder med. Hvis du vil vide, hvordan du finder den sværende tredje vinkel på en trekant, skal du se trin 1 for at komme i gang.

Metode En af tre:
Brug af de andre to vinkler

  1. 1 Tilføj de to kendte vinkelmålinger. Alt du skal vide er at alle vinklerne i en trekant altid Tilføj op til 180 °. Dette er sandt 100% af tiden. Så hvis du kender to af de tre målinger af trekanten, savner du kun ét stykke af puslespillet. Det første du kan gøre er at tilføje de vinkelmålinger, du kender. I dette eksempel er de to vinkelmålinger, du ved, 80 ° og 65 °. Tilføj dem (80 ° + 65 °) for at få 145 °.
  2. 2 Træk dette tal fra 180 °. Vinklerne i en trekant op til 180 °. Derfor er den resterende vinkel skal gøre summen op vinkler op til 180 °. I dette eksempel er 180 ° - 145 ° = 35 °.
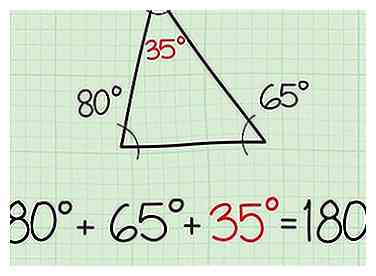  3. 3 Skriv ned dit svar. Du ved nu, at den tredje vinkel måler 35 °. Hvis du tvivler på dig selv, skal du bare tjekke dit arbejde. De tre vinkler skal tilføje op til 180 ° for at trianglen skal eksistere. 80 ° + 65 ° + 35 ° = 180 °. Du er færdig.

Metode To af tre:
Brug af variabler

  1. 1 Skriv ned problemet. Nogle gange, i stedet for at være heldige nok til at kende målingerne af to af vinklerne i en trekant, får du kun nogle få variabler, eller nogle variabler og en vinkelmåling. Lad os sige, at du arbejder med dette problem: Find målinger af vinkel "x" på trekanten, hvis målinger er "x," "2x" og 24. Først skal du bare skrive det ned.
  2. 2 Tilføj alle målinger. Det er det samme princip, som du ville følge, hvis du kendte målingerne af de to vinkler. Du skal blot tilføje målingen af ​​vinklerne og kombinere variablerne. Så, x + 2x + 24 ° = 3x + 24 °.
  3. 3 Træk målingerne fra 180 °. Træk nu disse målinger fra 180 ° for at komme nærmere løsningen af ​​problemet. Sørg for at sætte ligningen til 0. Det er sådan, hvordan det ser ud:
    • 180 ° - (3x + 24 °) = 0
    • 180 ° - 3x - 24 ° = 0
    • 156 ° - 3x = 0
  4. 4 Løs for x. Nu skal du blot sætte variablerne på den ene side af ligningen og tallene på den anden side. Du får 156 ° = 3x. Nu divider begge sider af ligningen med 3 for at få x = 52 °. Det betyder, at måling af den tredje vinkel på trekanten er 52 °. Den anden vinkel, 2x, er 2 x 52 ° eller 104 °.
  5. 5 Tjek dit arbejde. Hvis du vil sikre dig, at dette er en gyldig trekant, skal du blot tilføje de tre vinkelmålinger for at sikre, at de tilføjer op til 180 °. Det er 52 ° + 104 ° + 24 ° = 180 °. Du er færdig.

Metode Tre af tre:
Brug af andre metoder

  1. 1 Find den tredje vinkel af en enslig trekant. Isosceles triangler har to lige sider og to lige vinkler. De lige sider er markeret med et hashmærke på hver af dem, hvilket indikerer at vinklerne på tværs af hver side er ens. Hvis du kender vinkelmåling af en lige vinkel af en enslig trekant, så kender du måling af den anden lige vinkel. Sådan finder du det:
    • Hvis en af ​​de lige vinkler er 40 °, så ved du, at den anden vinkel også er 40 °. Du kan finde den tredje side, hvis det er nødvendigt, ved at trække 40 ° + 40 ° (som er 80 °) fra 180 °. 180 ° - 80 ° = 100 °, hvilket er måling af den resterende vinkel.
  2. 2 Find den tredje vinkel af en ligesidet trekant. En ligesidet trekant har alle lige sider og alle lige vinkler. Det vil typisk være markeret med to hash mærker midt på hver sin side. Dette betyder, at vinkelmåling af en hvilken som helst vinkel i en ligesidet trekant er 60 °. Tjek dit arbejde. 60 ° + 60 ° + 60 ° = 180 °.
  3. 3 Find den tredje vinkel af en ret trekant. Lad os sige, at du ved, at du har en rigtig trekant, hvor en af ​​de andre vinkler er 30 °. Hvis det er en rigtig trekant, så ved du, at en af ​​vinklerne måler nøjagtigt 90 °. De samme principper gælder. Alt du skal gøre er at tilføje målene på de sider, du kender (30 ° + 90 ° = 120 °) og trække det tal fra 180 °. Så, 180 ° - 120 ° = 60 °. Måling af den tredje vinkel er 60 °.