I geometri refererer udtrykket "perimeter" normalt til total afstand omkring ydersiden af en polygon, en 2-dimensionel form på 3 eller flere sider og vinkler. Med andre ord er en bestemt formes omkreds summen af længderne af alle dens sider. Den lethed, hvormed en formens omkreds kan findes, afhænger af flere faktorer - nemlig om polygonen er a fast polygon (en polygon hvis sider og vinkler er alle ens), og om ikke, om alle sidelængder i form er kendt. Hvis ingen af disse betingelser er sande, afhænger vanskeligheden ved at finde formens omkreds af, hvor meget information der er kendt om formen.
Steps
-
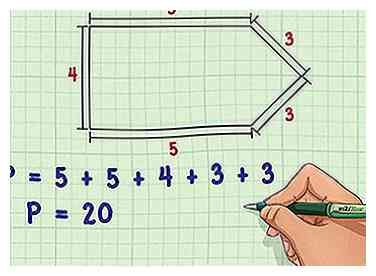 1 Find og tilføj længderne af alle polygonens sider. Omkredsen af nogen polygon kan beregnes ved at finde længden af hver side individuelt og derefter tilføje alle disse længder sammen. Dette er den mest enkle måde at finde en polygons omkreds på, og i former hvor ingen af siderne er ens, er det normalt den eneste nøjagtige måde at gøre det på.
1 Find og tilføj længderne af alle polygonens sider. Omkredsen af nogen polygon kan beregnes ved at finde længden af hver side individuelt og derefter tilføje alle disse længder sammen. Dette er den mest enkle måde at finde en polygons omkreds på, og i former hvor ingen af siderne er ens, er det normalt den eneste nøjagtige måde at gøre det på. - Som et simpelt eksempel vil en uregelmæssig polygon med sidelængder på 5, 5, 4, 3 og 3 have en omkreds på 5 + 5 + 4 + 3 + 3 = 20
- Hvis en eller flere af sidelængderne i din polygon er ukendte, kan processen til beregning af omkredsen blive vanskelig og kan kræve mere avanceret geometrisk viden. For eksempel, hvis din polygon er en rigtig trekant (eller kan opdeles i rigtige trekanter, kan trigonometri være et nyttigt værktøj til at finde længderne af ukendte sider, som forhindrer dig i at finde omkredsen af selve formen.
-
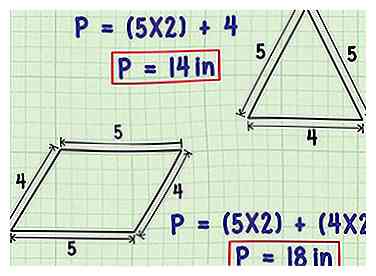 2 Multiplicér længderne af lige sider ved antallet af lige sider. Visse typer af polygoner har to eller flere lige sider. For eksempel har ligemønstre trekanter og ensidige trapezoider 2 af siderne af samme længde, mens parallelogrammer og rektangler har 2 par modstående sider med lige længde. I disse tilfælde, når du kender længden af en af de samme sider, kan du multiplicere denne længde med antallet af sider, der deler denne længde, og derefter tilføje længderne af eventuelle ulige sider for at finde omkredsen af den overordnede form.
2 Multiplicér længderne af lige sider ved antallet af lige sider. Visse typer af polygoner har to eller flere lige sider. For eksempel har ligemønstre trekanter og ensidige trapezoider 2 af siderne af samme længde, mens parallelogrammer og rektangler har 2 par modstående sider med lige længde. I disse tilfælde, når du kender længden af en af de samme sider, kan du multiplicere denne længde med antallet af sider, der deler denne længde, og derefter tilføje længderne af eventuelle ulige sider for at finde omkredsen af den overordnede form. - Lad os f.eks. Overveje en ensartet trekant, der har to sider med en længde på 5 inches (12,7 cm) og en side med en længde på 10 cm. Her for at finde omkredsen, ville vi tage længden af de lige sider (5) og multiplicere den med antallet af lige sider (2), og derefter tilføje længderne af den resterende ulige side. (5 × 2) + 4 = 10 + 4 = 14 tommer (35,6 cm).
- Som et eksempel på en form med flere par lige sider, lad os overveje et parallelogram med 2 sider med en længde på 5 inches (12,7 cm) og 2 med en længde på 4. For at finde omkredsen ville vi formere længden af længere side ved 2 og længden af den kortere side forbi, og tilføj derefter produkterne sammen. (2 × 5) + (2 × 4) = 10 + 8 = 18 inches (45,7 cm).
- Bemærk at denne metode også kan bruges til firkanter og rhombusser, som sammen med rektangler er særlige tilfælde af parallelogrammer.
-
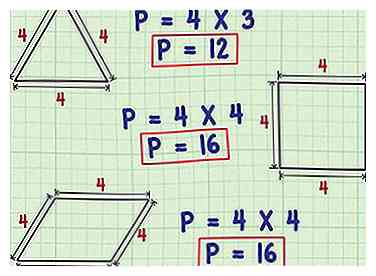 3 Multiplicér en regelmæssig polygon sidelængde ved antallet af sider. Polygoner, hvis sider er alle lige i længden og hvis vinkler er alle samme størrelse kaldes regelmæssige polygoner. F.eks. Er firkanter og ensidige trekanter almindelige polygoner, ligesom de er perfekte pentagoner (som eksemplificeret ved Chrysler-logoet) og ottekant (som eksemplificeret ved stopskilt). Hvis en form er en regelmæssig polygon, er det et simpelt spørgsmål at multiplicere længden af den ene side ved antallet af sider i formen.
3 Multiplicér en regelmæssig polygon sidelængde ved antallet af sider. Polygoner, hvis sider er alle lige i længden og hvis vinkler er alle samme størrelse kaldes regelmæssige polygoner. F.eks. Er firkanter og ensidige trekanter almindelige polygoner, ligesom de er perfekte pentagoner (som eksemplificeret ved Chrysler-logoet) og ottekant (som eksemplificeret ved stopskilt). Hvis en form er en regelmæssig polygon, er det et simpelt spørgsmål at multiplicere længden af den ene side ved antallet af sider i formen. - For eksempel er omkredsen af et perfekt firkant med en sidelængde på 4 inches (10,2 cm) 4 × 4 (fordi en firkant har 4 sider), eller 16 tommer (40,6 cm), mens omkredsen af en ligesidet trekant med en sidelængde på 4 inches (10,2 cm) er 4 × 3, eller 12 inches (30,5 cm).
- Den samme grundlæggende proces virker også for ikke-regulære polygoner, hvis sider alle har lige længder. For eksempel, selvom en rhombus ikke er en regelmæssig polygon, fordi dens vinkler ikke er af samme størrelse, kan du finde sin omkreds ved at gange længden af den ene side af antallet af sider, fordi alle 4 sider er af samme længde.
-
 4 Alternativt kan du bruge området og apothem af en regelmæssig polygon for at finde sin omkreds. Selvom man blot multiplicerer længden af en af en regelmæssig polygons sider ved antallet af sider i polygonen er den nemmeste måde at finde sin omkreds på, er det ikke den eneste vej. Afstanden fra polygonens centrum til den nøjagtige midten af en af siderne, kaldet apothem, er en del af en ligning, der giver dig mulighed for at finde sin omkreds, forudsat at du også kender polygonens område. Indsætte kendte værdier for område og apotem i ligningen (Areal) = (Perimeter) × (Apothem) / 2 giver dig mulighed for at løse polygonens område ved hjælp af simpel algebra.
4 Alternativt kan du bruge området og apothem af en regelmæssig polygon for at finde sin omkreds. Selvom man blot multiplicerer længden af en af en regelmæssig polygons sider ved antallet af sider i polygonen er den nemmeste måde at finde sin omkreds på, er det ikke den eneste vej. Afstanden fra polygonens centrum til den nøjagtige midten af en af siderne, kaldet apothem, er en del af en ligning, der giver dig mulighed for at finde sin omkreds, forudsat at du også kender polygonens område. Indsætte kendte værdier for område og apotem i ligningen (Areal) = (Perimeter) × (Apothem) / 2 giver dig mulighed for at løse polygonens område ved hjælp af simpel algebra. - F.eks. Har firkanten med en sidelængde på 4 tommer (10,2 cm) i ovenstående eksempel et område på 16 tommer2 og en apothem på 2 inches (5.1 cm). Ved hjælp af vores nye ligning løser vi for omkredsen som følger:
- 16 = (omkreds) × 2/2
- 16 = (omkreds) × 1
- 16 = omkreds. Firkantets perimeter er 16 tommer (40,6 cm) - Dette er det samme svar, som vi fik over med standardmetoden.
- F.eks. Har firkanten med en sidelængde på 4 tommer (10,2 cm) i ovenstående eksempel et område på 16 tommer2 og en apothem på 2 inches (5.1 cm). Ved hjælp af vores nye ligning løser vi for omkredsen som følger:
 Minotauromaquia
Minotauromaquia
 1 Find og tilføj længderne af alle polygonens sider. Omkredsen af nogen polygon kan beregnes ved at finde længden af hver side individuelt og derefter tilføje alle disse længder sammen. Dette er den mest enkle måde at finde en polygons omkreds på, og i former hvor ingen af siderne er ens, er det normalt den eneste nøjagtige måde at gøre det på.
1 Find og tilføj længderne af alle polygonens sider. Omkredsen af nogen polygon kan beregnes ved at finde længden af hver side individuelt og derefter tilføje alle disse længder sammen. Dette er den mest enkle måde at finde en polygons omkreds på, og i former hvor ingen af siderne er ens, er det normalt den eneste nøjagtige måde at gøre det på.  2 Multiplicér længderne af lige sider ved antallet af lige sider. Visse typer af polygoner har to eller flere lige sider. For eksempel har ligemønstre trekanter og ensidige trapezoider 2 af siderne af samme længde, mens parallelogrammer og rektangler har 2 par modstående sider med lige længde. I disse tilfælde, når du kender længden af en af de samme sider, kan du multiplicere denne længde med antallet af sider, der deler denne længde, og derefter tilføje længderne af eventuelle ulige sider for at finde omkredsen af den overordnede form.
2 Multiplicér længderne af lige sider ved antallet af lige sider. Visse typer af polygoner har to eller flere lige sider. For eksempel har ligemønstre trekanter og ensidige trapezoider 2 af siderne af samme længde, mens parallelogrammer og rektangler har 2 par modstående sider med lige længde. I disse tilfælde, når du kender længden af en af de samme sider, kan du multiplicere denne længde med antallet af sider, der deler denne længde, og derefter tilføje længderne af eventuelle ulige sider for at finde omkredsen af den overordnede form.  3 Multiplicér en regelmæssig polygon sidelængde ved antallet af sider. Polygoner, hvis sider er alle lige i længden og hvis vinkler er alle samme størrelse kaldes regelmæssige polygoner. F.eks. Er firkanter og ensidige trekanter almindelige polygoner, ligesom de er perfekte pentagoner (som eksemplificeret ved Chrysler-logoet) og ottekant (som eksemplificeret ved stopskilt). Hvis en form er en regelmæssig polygon, er det et simpelt spørgsmål at multiplicere længden af den ene side ved antallet af sider i formen.
3 Multiplicér en regelmæssig polygon sidelængde ved antallet af sider. Polygoner, hvis sider er alle lige i længden og hvis vinkler er alle samme størrelse kaldes regelmæssige polygoner. F.eks. Er firkanter og ensidige trekanter almindelige polygoner, ligesom de er perfekte pentagoner (som eksemplificeret ved Chrysler-logoet) og ottekant (som eksemplificeret ved stopskilt). Hvis en form er en regelmæssig polygon, er det et simpelt spørgsmål at multiplicere længden af den ene side ved antallet af sider i formen.  4 Alternativt kan du bruge området og apothem af en regelmæssig polygon for at finde sin omkreds. Selvom man blot multiplicerer længden af en af en regelmæssig polygons sider ved antallet af sider i polygonen er den nemmeste måde at finde sin omkreds på, er det ikke den eneste vej. Afstanden fra polygonens centrum til den nøjagtige midten af en af siderne, kaldet apothem, er en del af en ligning, der giver dig mulighed for at finde sin omkreds, forudsat at du også kender polygonens område. Indsætte kendte værdier for område og apotem i ligningen (Areal) = (Perimeter) × (Apothem) / 2 giver dig mulighed for at løse polygonens område ved hjælp af simpel algebra.
4 Alternativt kan du bruge området og apothem af en regelmæssig polygon for at finde sin omkreds. Selvom man blot multiplicerer længden af en af en regelmæssig polygons sider ved antallet af sider i polygonen er den nemmeste måde at finde sin omkreds på, er det ikke den eneste vej. Afstanden fra polygonens centrum til den nøjagtige midten af en af siderne, kaldet apothem, er en del af en ligning, der giver dig mulighed for at finde sin omkreds, forudsat at du også kender polygonens område. Indsætte kendte værdier for område og apotem i ligningen (Areal) = (Perimeter) × (Apothem) / 2 giver dig mulighed for at løse polygonens område ved hjælp af simpel algebra.