Denne metode til multiplikation og division blev brugt af Descartes og er fra Euclids "Elements", Bog VI, Proposition 12. Den er baseret på lignende trekanter. Det kan meget vel være den måde, som mor naturen udfører multiplikation og division! Man forestiller sig, at naturen kan skabe lige linjer gennem udledning af hurtige vibrationer gennem tæt pakket partikler eller molekyler. Se artiklen Center a Circle og tænk hvordan det kan fungere i omvendt for at opnå netop dette krav. Dette er dog kun en teori, en mulighed; Videnskaben ved, at naturen udfører matematiske vidundere, såsom phyllotaxier og vækstmønstre meget som fraktal iterative mønstre, men diskuterer stadig, hvordan hun udfører det! Det er værd at tænke på og udtænke eksperimenter og empiriske beviser for bevis.

Steps

  • Bliv bekendt med billedet af det grundlæggende koncept: 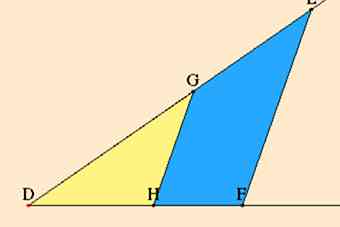Lignende Triangler

Første del af tre:
Tutorial

  1. 1 Se på disse lignende trekanter, og derfor andelen DG / DH = DE / DF. Lignende Triangler Du kan bruge den til at udføre multiplikation og division. Åbn en ny projektmappe i Excel og kopier tegningen.
  2. 2 For at multiplicere x gange y, lav horisontal linje DH med længde 1, forlæng DF med længde x fra DH og hæv DG af længde y i en vinkel over vandret DF. Tegn HG og konstruer en linje gennem F parallelt med HG. Lad det krydse DG ved E. Så vil DE have længde xy.
  3. 3 At dividere y med x, lav DH med længde 1, DF med længde x og DE med længde y. Tegn EF og konstruer en linje gennem H parallelt med EF. Lad det krydse DE ved G. Derefter vil DG have længde y / x.
  4. 4 Antag en stamme eller et blad der ligger bag en anden i sin skygge. Kan dette muligvis være en måde at holde tid på og "vide, hvornår man skal flytte til side" for at opnå bedre lys direkte for det nedre blad eller stammen?
  5. 5 Antag at krydse rødder (som de gør) og antage en vis følsomhed for hinanden - kan det være sådan, at planter udfører matematik og sender vigtige næringsstoffer rettidigt op i planterne? Trods alt er rødderne i mørke, hvordan ved de, hvad tid det er eller beregner andelen af ​​en given kemisk blanding at sende?
  6. 6 Antag, at neuroner forgrener sig i forskellige vinkler i hjernen (som de gør) - kan dette være en måde at beregne p / n = A.E.N. (Næsten ethvert tal)? Det vil sige, at næsten ethvert tal kan udtrykkes som et kvotient af to andre tal, f.eks. 36/2 = 18 og 625/256 = 2.44140625 eller 5 ^ 4/4 ^ 4 eller 5/4 ^ (1 / (5/4 - 1)). Se artiklen Start med at arbejde med fortsatte fraktioner og løst aB = a ^ B i neutrale operationer Brug algebra hvor det diskuterer E = mc ^ n som n nærmer sig 2. Er det muligt at "se i går" i hukommelsen ved at se langsommere end stoppet tid med let hastighed firkantet? Er "Past" på den modsatte side af alle elektroner overfor mig, og "Fremtiden" spinder rundt fra den modsatte position for at hilse på mig også? Det ville gøre den umiddelbare fortid meget ligesom den umiddelbare fremtid, hvilket resulterer i et forholdsvis stabilt nutid. Og geometrisk vil alle stråler fra alle de partikler, der kommer igennem i vibrationer, blive forholdsvis konstant multipliceret og opdelt så godt, så længe man er temmelig stille eller i et relativt stabilt miljø. Kald dette "The Supposition About Neurons and Neutrons", hvis du vil.
  7. 7Descartes brugte også det næste forslag, VI.13, for at tage firkantede rødder geometrisk.

Del to af tre:
Bliv nysgerrig

  1. 1 Hvis det kan gøres geometrisk, kan Mother Nature udføre det inden for rimelige tolerancer? Det vil sige, kan hun få rimelige skøn over kvadratroden eller en hvilken som helst rod af et tal? Man overbeviser "enhver rod" fra at antage en iterativ proces (der forekom tilsyneladende ikke Euclid, Descartes eller Newton-Raphson).
  2. 2 Endeligt billede: Lignende Triangler

Del tre af tre:
Nyttig vejledning

  1. 1 Gør brug af hjælperartikler, når du fortsætter gennem denne vejledning:
    • Se artiklen Sådan oprettes en Spirallic Spin Particle Path eller Halskæde Form eller Sfærisk Border for en liste over artikler relateret til Excel, Geometrisk og / eller Trigonometrisk Kunst, Kortlægning / Diagrammering og Algebraisk Formulering.
    • For flere kunstdiagrammer og grafer kan du også klikke på Kategori: Microsoft Excel Imagery, Kategori: Matematik, Kategori: Regneark eller Kategori: Grafik for at se mange Excel regneark og diagrammer, hvor Trigonometri, Geometri og Calculus er blevet omdannet til Kunst, eller klik blot på kategorien som vist i øverste højre hvide del af denne side eller nederst til venstre på siden.