I modsætning til en lige linje ændres en kurves hældning konstant, mens du bevæger dig langs grafen. Calculus introducerer eleverne til ideen om, at hvert punkt på denne graf kunne beskrives med en hældning eller en "øjeblikkelig ændringstakt". Tangentlinjen er en lige linje med den hældning, der passerer gennem det nøjagtige punkt på grafen. For at finde ligningen for tangenten skal du vide, hvordan du tager derivatet af den oprindelige ligning.
Metode En af To:
Find ligningen af en tangentlinie
-
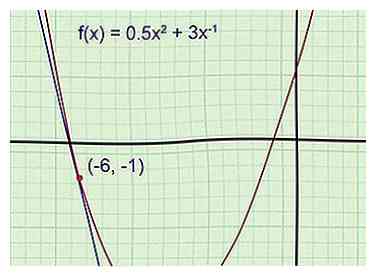 1 Skitse funktionen og tangentlinjen (anbefales). En graf gør det nemmere at følge problemet og kontrollere, om svaret giver mening. Skitse funktionen på et stykke grafpapir, ved hjælp af en grafisk regnemaskine som reference, hvis det er nødvendigt. Skits tangentlinjen gennem det givne punkt. (Husk, at tangentlinjen løber gennem det punkt og har samme hældning som grafen på det tidspunkt.)
1 Skitse funktionen og tangentlinjen (anbefales). En graf gør det nemmere at følge problemet og kontrollere, om svaret giver mening. Skitse funktionen på et stykke grafpapir, ved hjælp af en grafisk regnemaskine som reference, hvis det er nødvendigt. Skits tangentlinjen gennem det givne punkt. (Husk, at tangentlinjen løber gennem det punkt og har samme hældning som grafen på det tidspunkt.) - Eksempel 1: Skitse grafen af parabolen . Tegn tangenten igennem punktet (-6, -1).
Du kender ikke tangentens ligning endnu, men du kan allerede fortælle, at dens hældning er negativ, og at dens y-afsnit er negativ (langt under parabola-vertexet med y-værdi -5,5). Hvis dit endelige svar ikke stemmer overens med disse oplysninger, vil du vide for at kontrollere dit arbejde for fejl.
- Eksempel 1: Skitse grafen af parabolen . Tegn tangenten igennem punktet (-6, -1).
-
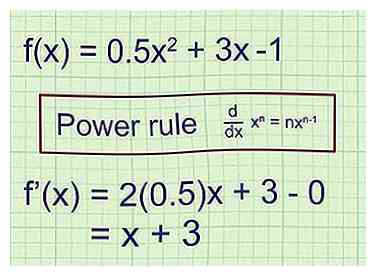 2 Tag det første derivat for at finde ligningen for hældning af tangentlinjen. For funktion f (x) repræsenterer det første derivat f '(x) ligningen for hældningen af tangentlinjen på et hvilket som helst punkt på f (x). Der er mange måder at tage derivater på. Her er et simpelt eksempel ved brug af strømreglen:[1]
2 Tag det første derivat for at finde ligningen for hældning af tangentlinjen. For funktion f (x) repræsenterer det første derivat f '(x) ligningen for hældningen af tangentlinjen på et hvilket som helst punkt på f (x). Der er mange måder at tage derivater på. Her er et simpelt eksempel ved brug af strømreglen:[1] - Eksempel 1 (forts.): Grafen beskrives af funktionen .
Husk strømreglen, når du tager derivater: .
Funktionens første derivat = f '(x) = (2) (0,5) x + 3 - 0.
f '(x) = x + 3. Plug enhver værdi a for x i denne ligning, og resultatet vil være hældningen af linjeknappen til f (x) ved punktet x = a.
- Eksempel 1 (forts.): Grafen beskrives af funktionen .
-
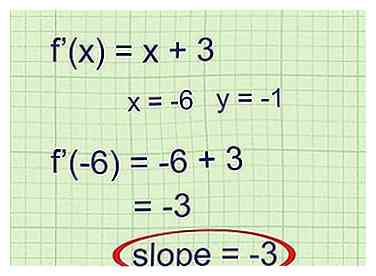 3 Indtast x-værdien af det punkt, du undersøger. Læs problemet for at finde koordinaterne for det punkt, hvor du finder tangentlinjen. Indtast x-koordinatet for dette punkt i f '(x). Udgangen er hældningen af tangentlinjen på dette punkt.
3 Indtast x-værdien af det punkt, du undersøger. Læs problemet for at finde koordinaterne for det punkt, hvor du finder tangentlinjen. Indtast x-koordinatet for dette punkt i f '(x). Udgangen er hældningen af tangentlinjen på dette punkt. - Eksempel 1 (forts.): Det punkt, der er nævnt i problemet, er (-6, -1). Brug x-koordinaten -6 som input for f '(x):
f '(- 6) = -6 + 3 = -3
Hældningen af tangentlinjen er -3.
- Eksempel 1 (forts.): Det punkt, der er nævnt i problemet, er (-6, -1). Brug x-koordinaten -6 som input for f '(x):
-
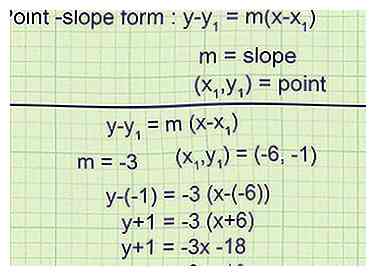 4 Skriv tangentlinjens ligning i punkt-skråning form. Point-hældningsformen af en lineær ligning er , hvor m er hældningen og er et punkt på linjen.[2] Du har nu alle de oplysninger, du har brug for til at skrive tangentlinjens ligning i denne formular.
4 Skriv tangentlinjens ligning i punkt-skråning form. Point-hældningsformen af en lineær ligning er , hvor m er hældningen og er et punkt på linjen.[2] Du har nu alle de oplysninger, du har brug for til at skrive tangentlinjens ligning i denne formular. - Eksempel 1 (forts.):
Hældningen af linjen er -3, så
Tangentlinjen passerer gennem (-6, -1), så den endelige ligning er
Forenkle til
- Eksempel 1 (forts.):
-
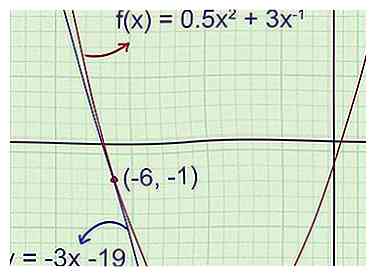 5 Bekræft ligningen på din graf. Hvis du har en grafisk regnemaskine, graver du den oprindelige funktion og tangentlinjen for at kontrollere, at du har det rigtige svar. Hvis du arbejder på papir, skal du henvise til din tidligere graf for at sikre, at der ikke er nogen klare fejl i dit svar.
5 Bekræft ligningen på din graf. Hvis du har en grafisk regnemaskine, graver du den oprindelige funktion og tangentlinjen for at kontrollere, at du har det rigtige svar. Hvis du arbejder på papir, skal du henvise til din tidligere graf for at sikre, at der ikke er nogen klare fejl i dit svar. - Eksempel 1 (forts.): Den oprindelige skitse viste, at tangentlinjens hældning var negativ, og y-interceptet var godt under -5,5. Tangentlinjens ligning er fundet y = -3x - 19 i hældningsaflytningsform, hvilket betyder -3 er hældningen og -19 er y-afsnit. Begge disse attributter matcher de oprindelige forudsigelser.
-
 6 Prøv et vanskeligere problem. Her er en gennemgang af hele processen igen. Denne gang er målet at finde linjen tangent til ved x = 2:
6 Prøv et vanskeligere problem. Her er en gennemgang af hele processen igen. Denne gang er målet at finde linjen tangent til ved x = 2: - Brug af strømreglen, det første derivat . Denne funktion vil fortælle os hældningen af tangenten.
- Siden x = 2 finder du . Dette er hældningen ved x = 2.
- Bemærk, at vi ikke har et punkt denne gang, kun en x-koordinat. For at finde y-koordinatet, sæt x = 2 i den indledende funktion: . Pointen er (2,27).
- Skriv tangentlinjens ligning i punkt-skråning form:
Om nødvendigt forenkles til y = 25x - 23.
Metode To af to:
Løsning af relaterede problemer
-
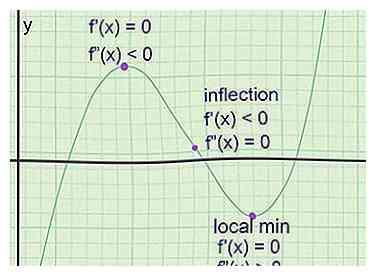 1 Find de ekstreme punkter på en graf. Dette er punkter, hvor grafen når et lokalt maksimum (et punkt højere end punkterne på begge sider) eller lokalt minimum (lavere end punkterne på begge sider). Tangentlinjen har altid en hældning på 0 på disse punkter (en vandret linje), men en nulhældning alene garanterer ikke et ekstremt punkt. Sådan finder du dem:[3]
1 Find de ekstreme punkter på en graf. Dette er punkter, hvor grafen når et lokalt maksimum (et punkt højere end punkterne på begge sider) eller lokalt minimum (lavere end punkterne på begge sider). Tangentlinjen har altid en hældning på 0 på disse punkter (en vandret linje), men en nulhældning alene garanterer ikke et ekstremt punkt. Sådan finder du dem:[3] - Tag det første derivat af funktionen for at få f '(x), ligningen for tangentens hældning.
- Løs for f '(x) = 0 for at finde muligt ekstreme punkter.
- Tag det andet derivat for at få f "(x), ligningen, der fortæller dig, hvor hurtigt tangens hældning ændrer sig.
- For hvert muligt ekstrempunkt skal du stikke x-koordinaten -en ind i f "(x). Hvis f" (a) er positiv, er der et lokalt minimum på -en. Hvis f "(a) er negativ, er der et lokalt maksimum. Hvis f" (a) er 0, er der et bøjningspunkt, ikke et ekstremt punkt.
- Hvis der er et maksimum eller minimum på -en, find f (a) for at få y-koordinaten.
-
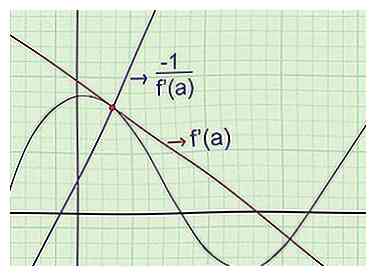 2 Find ligningen af det normale. Den "normale" til en kurve på et bestemt punkt går gennem det punkt, men har en skråning vinkelret på en tangent. For at finde ligningen for det normale, drage fordel af det faktum, at (hældning af tangent) (normal hældning) = -1, når de begge passerer gennem samme punkt på grafen.[4] Med andre ord:
2 Find ligningen af det normale. Den "normale" til en kurve på et bestemt punkt går gennem det punkt, men har en skråning vinkelret på en tangent. For at finde ligningen for det normale, drage fordel af det faktum, at (hældning af tangent) (normal hældning) = -1, når de begge passerer gennem samme punkt på grafen.[4] Med andre ord: - Find f '(x), hældningen af tangentlinjen.
- Hvis punktet er ved x = -en, find f '(a) for at finde hældningen af tangenten på det tidspunkt.
- Beregn for at finde hældningen af det normale.
- Skriv den normale ligning i hældningspunktform.
Facebook
Twitter
Google+
 Minotauromaquia
Minotauromaquia
 1 Skitse funktionen og tangentlinjen (anbefales). En graf gør det nemmere at følge problemet og kontrollere, om svaret giver mening. Skitse funktionen på et stykke grafpapir, ved hjælp af en grafisk regnemaskine som reference, hvis det er nødvendigt. Skits tangentlinjen gennem det givne punkt. (Husk, at tangentlinjen løber gennem det punkt og har samme hældning som grafen på det tidspunkt.)
1 Skitse funktionen og tangentlinjen (anbefales). En graf gør det nemmere at følge problemet og kontrollere, om svaret giver mening. Skitse funktionen på et stykke grafpapir, ved hjælp af en grafisk regnemaskine som reference, hvis det er nødvendigt. Skits tangentlinjen gennem det givne punkt. (Husk, at tangentlinjen løber gennem det punkt og har samme hældning som grafen på det tidspunkt.) 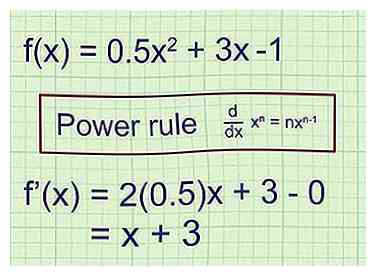 2 Tag det første derivat for at finde ligningen for hældning af tangentlinjen. For funktion f (x) repræsenterer det første derivat f '(x) ligningen for hældningen af tangentlinjen på et hvilket som helst punkt på f (x). Der er mange måder at tage derivater på. Her er et simpelt eksempel ved brug af strømreglen:[1]
2 Tag det første derivat for at finde ligningen for hældning af tangentlinjen. For funktion f (x) repræsenterer det første derivat f '(x) ligningen for hældningen af tangentlinjen på et hvilket som helst punkt på f (x). Der er mange måder at tage derivater på. Her er et simpelt eksempel ved brug af strømreglen:[1] 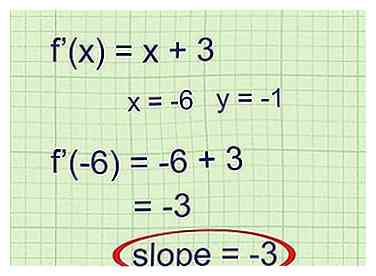 3 Indtast x-værdien af det punkt, du undersøger. Læs problemet for at finde koordinaterne for det punkt, hvor du finder tangentlinjen. Indtast x-koordinatet for dette punkt i f '(x). Udgangen er hældningen af tangentlinjen på dette punkt.
3 Indtast x-værdien af det punkt, du undersøger. Læs problemet for at finde koordinaterne for det punkt, hvor du finder tangentlinjen. Indtast x-koordinatet for dette punkt i f '(x). Udgangen er hældningen af tangentlinjen på dette punkt. 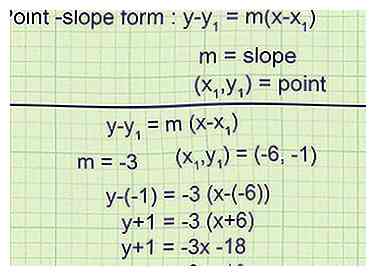 4 Skriv tangentlinjens ligning i punkt-skråning form. Point-hældningsformen af en lineær ligning er
4 Skriv tangentlinjens ligning i punkt-skråning form. Point-hældningsformen af en lineær ligning er  5 Bekræft ligningen på din graf. Hvis du har en grafisk regnemaskine, graver du den oprindelige funktion og tangentlinjen for at kontrollere, at du har det rigtige svar. Hvis du arbejder på papir, skal du henvise til din tidligere graf for at sikre, at der ikke er nogen klare fejl i dit svar.
5 Bekræft ligningen på din graf. Hvis du har en grafisk regnemaskine, graver du den oprindelige funktion og tangentlinjen for at kontrollere, at du har det rigtige svar. Hvis du arbejder på papir, skal du henvise til din tidligere graf for at sikre, at der ikke er nogen klare fejl i dit svar.  6 Prøv et vanskeligere problem. Her er en gennemgang af hele processen igen. Denne gang er målet at finde linjen tangent til
6 Prøv et vanskeligere problem. Her er en gennemgang af hele processen igen. Denne gang er målet at finde linjen tangent til  1 Find de ekstreme punkter på en graf. Dette er punkter, hvor grafen når et lokalt maksimum (et punkt højere end punkterne på begge sider) eller lokalt minimum (lavere end punkterne på begge sider). Tangentlinjen har altid en hældning på 0 på disse punkter (en vandret linje), men en nulhældning alene garanterer ikke et ekstremt punkt. Sådan finder du dem:[3]
1 Find de ekstreme punkter på en graf. Dette er punkter, hvor grafen når et lokalt maksimum (et punkt højere end punkterne på begge sider) eller lokalt minimum (lavere end punkterne på begge sider). Tangentlinjen har altid en hældning på 0 på disse punkter (en vandret linje), men en nulhældning alene garanterer ikke et ekstremt punkt. Sådan finder du dem:[3]  2 Find ligningen af det normale. Den "normale" til en kurve på et bestemt punkt går gennem det punkt, men har en skråning vinkelret på en tangent. For at finde ligningen for det normale, drage fordel af det faktum, at (hældning af tangent) (normal hældning) = -1, når de begge passerer gennem samme punkt på grafen.[4] Med andre ord:
2 Find ligningen af det normale. Den "normale" til en kurve på et bestemt punkt går gennem det punkt, men har en skråning vinkelret på en tangent. For at finde ligningen for det normale, drage fordel af det faktum, at (hældning af tangent) (normal hældning) = -1, når de begge passerer gennem samme punkt på grafen.[4] Med andre ord: