Radens kugle (forkortet som variablen r eller R) er afstanden fra det nøjagtige centrum af kuglen til et punkt på den udvendige kant af den kugle. Som med cirkler er radius af en kugle ofte et væsentligt stykke startinformation til beregning af formens diameter, omkreds, overflade og / eller volumen. Du kan dog også arbejde baglæns fra diameter, omkreds osv. For at finde kugles radius. Brug formlen, der virker med de oplysninger, du har.
Metode En af tre:
Brug af Radius Beregnings Formler
-
 1 Find radius, hvis du kender diameteren. Radien er halve diameteren, så brug formlen r = D / 2. Dette er identisk med metoden til beregning af en cirkels radius fra dens diameter.[1]
1 Find radius, hvis du kender diameteren. Radien er halve diameteren, så brug formlen r = D / 2. Dette er identisk med metoden til beregning af en cirkels radius fra dens diameter.[1] - Hvis du har en kugle med en diameter på 16 cm, find radius ved at dividere 16/2 for at få 8 cm. Hvis diameteren er 42, så er radiusen 21.
-
 2 Find radiusen, hvis du kender omkredsen. Brug formlen C / 2π. Da omkredsen er lig med πD, som er lig med 2πr, vil opdeling af omkredsen med 2π give radius.[2]
2 Find radiusen, hvis du kender omkredsen. Brug formlen C / 2π. Da omkredsen er lig med πD, som er lig med 2πr, vil opdeling af omkredsen med 2π give radius.[2] - Hvis du har en kugle med en omkreds på 20 m, find radius ved at dividere 20 / 2π = 3.183 m.
- Brug den samme formel til at konvertere mellem radius og omkreds af en cirkel.
-
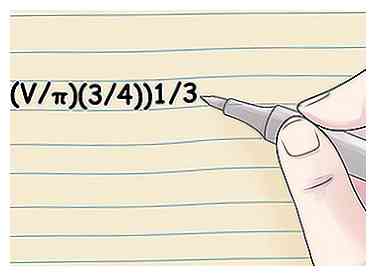 3 Beregn radius, hvis du kender en sfære. Brug formlen ((V / π) (3/4))1/3.[3] Volumenet af en kugle er afledt af ligningen V = (4/3) πr3. Løsning for r-variablen i denne ligning får ((V / π) (3/4))1/3 = r, hvilket betyder at radius af en kugle er lig med volumen divideret med π, gange 3/4, alt taget til 1/3 effekten (eller kubuskottet.)[4]
3 Beregn radius, hvis du kender en sfære. Brug formlen ((V / π) (3/4))1/3.[3] Volumenet af en kugle er afledt af ligningen V = (4/3) πr3. Løsning for r-variablen i denne ligning får ((V / π) (3/4))1/3 = r, hvilket betyder at radius af en kugle er lig med volumen divideret med π, gange 3/4, alt taget til 1/3 effekten (eller kubuskottet.)[4] - Hvis du har en kugle med et volumen på 100 inches3, løse for radius som følger:
- ((V / π) (3/4))1/3 = r
- ((100/π)(3/4))1/3 = r
- ((31.83)(3/4))1/3 = r
- (23.87)1/3 = r
- 2,88 in = r
- Hvis du har en kugle med et volumen på 100 inches3, løse for radius som følger:
-
 4 Find radius fra overfladeområdet. Brug formlen r = √ (A / (4π)). Overfladearealet af en kugle er afledt af ligningen A = 4πr2. Løsningen for r-variablen giver √ (A / (4π)) = r, hvilket betyder at en radius radius svarer til kvadratroten af overfladeområdet divideret med 4π. Du kan også tage (A / (4π)) til 1/2 strøm til det samme resultat.[5]
4 Find radius fra overfladeområdet. Brug formlen r = √ (A / (4π)). Overfladearealet af en kugle er afledt af ligningen A = 4πr2. Løsningen for r-variablen giver √ (A / (4π)) = r, hvilket betyder at en radius radius svarer til kvadratroten af overfladeområdet divideret med 4π. Du kan også tage (A / (4π)) til 1/2 strøm til det samme resultat.[5] - Hvis du har en kugle med et overflade på 1.200 cm2, løse for radius som følger:
- √ (A / (4π)) = r
- √ (1200 / (4π)) = r
- √ (300 / (π)) = r
- √ (95,49) = r
- 9,77 cm = r
- Hvis du har en kugle med et overflade på 1.200 cm2, løse for radius som følger:
Metode To af tre:
Definere nøglebegreber
-
 1 Identificer de grundlæggende målinger af en kugle. Radien (r) er afstanden fra det nøjagtige centrum af kuglen til ethvert punkt på kuglens overflade. Generelt kan du finde radius af en kugle, hvis du kender diameteren, omkredsen, lydstyrken eller overfladearealet.
1 Identificer de grundlæggende målinger af en kugle. Radien (r) er afstanden fra det nøjagtige centrum af kuglen til ethvert punkt på kuglens overflade. Generelt kan du finde radius af en kugle, hvis du kender diameteren, omkredsen, lydstyrken eller overfladearealet. - Diameter (D): afstanden over kuglen - dobbelt radius. Diameter er længden af en linje gennem centrum af kuglen: fra et punkt på kuglens udside til et tilsvarende punkt direkte overfor det. Med andre ord, den største mulige afstand mellem to punkter på kuglen.
- Omkreds (C): den endimensionelle afstand rundt om kuglen på det bredeste punkt. Med andre ord, omkredsen af et sfærisk tværsnit, hvis plan passerer gennem centrum af kuglen.
- Volumen (V): Det tredimensionale rum indeholdt i kuglen. Det er det "rum, som kuglen tager op."[6]
- Overfladeareal (A): Det todimensionale område på kuglens yderside. Mængden af fladt rum, der dækker kuglens yderside.
- Pi (π): en konstant, der udtrykker forholdet mellem cirkelens omkreds og cirkelens diameter. De første ti cifre i Pi er altid 3.141592653, selv om det normalt afrundes til 3.14.
-
 2 Brug forskellige målinger til at finde radius. Du kan bruge diameteren, omkredsen, volumenet og overfladeområdet til at beregne radius af en kugle. Du kan også beregne hvert af disse tal, hvis du kender længden af radiusen selv. For at finde radiusen, så prøv at vende formlerne til disse komponenters beregninger. Lær formlerne, der bruger radiusen for at finde diameter, omkreds, volumen og overfladeareal.
2 Brug forskellige målinger til at finde radius. Du kan bruge diameteren, omkredsen, volumenet og overfladeområdet til at beregne radius af en kugle. Du kan også beregne hvert af disse tal, hvis du kender længden af radiusen selv. For at finde radiusen, så prøv at vende formlerne til disse komponenters beregninger. Lær formlerne, der bruger radiusen for at finde diameter, omkreds, volumen og overfladeareal. - D = 2r. Som med cirkler er diameteren af en kugle to gange radius.
- C = πD eller 2πr. Som med cirkler er omkredsen af en kugle lig med π gange diameteren. Da diameteren er to gange radiusen, kan vi også sige at omkredsen er to gange radius gange π.
- V = (4/3) πr3. Kuglens volumen er radiusen kuberet (gange selv to gange), gange π, gange 4/3.[7]
- A = 4πr2. Overfladearealet af en kugle er radiusen kvadret (gange i sig selv), gange π, gange 4. Da området af en cirkel er πr2, kan det også siges, at en kugles overflade er fire gange det område af cirklen dannet af dens omkreds.
Metode Tre af tre:
Find radius som afstanden mellem to punkter
-
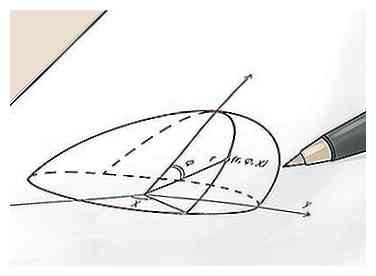 1 Find (x, y, z) koordinaterne for kuglens centrale punkt. En måde at tænke på radius af en kugle er som afstanden mellem punktet i centrum af kuglen og et hvilket som helst punkt på kuglens overflade. Fordi dette er sandt, hvis du kender punktets koordinater i centrum af kuglen og af ethvert punkt på overfladen, kan du finde kuglens radius ved blot at beregne afstanden mellem de to punkter med en variant af de grundlæggende afstand formel. For at begynde, find koordinaterne for kugles midtpunkt. Bemærk, at fordi kugler er tredimensionale, vil dette være et (x, y, z) punkt snarere end et (x, y) punkt.
1 Find (x, y, z) koordinaterne for kuglens centrale punkt. En måde at tænke på radius af en kugle er som afstanden mellem punktet i centrum af kuglen og et hvilket som helst punkt på kuglens overflade. Fordi dette er sandt, hvis du kender punktets koordinater i centrum af kuglen og af ethvert punkt på overfladen, kan du finde kuglens radius ved blot at beregne afstanden mellem de to punkter med en variant af de grundlæggende afstand formel. For at begynde, find koordinaterne for kugles midtpunkt. Bemærk, at fordi kugler er tredimensionale, vil dette være et (x, y, z) punkt snarere end et (x, y) punkt. - Denne proces er lettere at forstå ved at følge med et eksempel. Til vores formål, lad os sige, at vi har en kugle centreret omkring (x, y, z) punktet (4, -1, 12). I de næste trin bruger vi dette punkt til at finde radiusen.
-
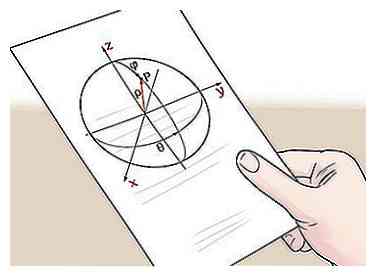 2 Find koordinaterne for et punkt på overfladen af kuglen. Dernæst skal du finde (x, y, z) koordinaterne for et punkt på overfladen af kuglen. Dette kan være nogen peg på overfladen af kuglen. Fordi punkterne på overfladen af en kugle er ækvivalente fra midten punkt pr. Definition, vil ethvert punkt arbejde for at bestemme radiusen.
2 Find koordinaterne for et punkt på overfladen af kuglen. Dernæst skal du finde (x, y, z) koordinaterne for et punkt på overfladen af kuglen. Dette kan være nogen peg på overfladen af kuglen. Fordi punkterne på overfladen af en kugle er ækvivalente fra midten punkt pr. Definition, vil ethvert punkt arbejde for at bestemme radiusen. - Med henblik på vores eksempel problem, lad os sige, at vi ved det punktet (3, 3, 0) ligger på overfladen af kuglen. Ved at beregne afstanden mellem dette punkt og midtpunktet, kan vi finde radius.
-
 3 Find radius med formlen d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Nu hvor du kender midten af kuglen og et punkt på overfladen, vil beregningen af afstanden mellem de to finde radius. Brug den tredimensionelle afstandsformel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), hvor d er lig med afstand, (x1, y1, z1) er lig med koordinaterne for midtpunktet, og (x2, y2, z2) er lig med koordinaterne for punktet på overfladen for at finde afstanden mellem de to punkter.
3 Find radius med formlen d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Nu hvor du kender midten af kuglen og et punkt på overfladen, vil beregningen af afstanden mellem de to finde radius. Brug den tredimensionelle afstandsformel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), hvor d er lig med afstand, (x1, y1, z1) er lig med koordinaterne for midtpunktet, og (x2, y2, z2) er lig med koordinaterne for punktet på overfladen for at finde afstanden mellem de to punkter. - I vores eksempel ville vi plugge (4, -1, 12) til (x1, y1, z1) og (3, 3, 0) for (x2, y2, z2), løsningen som følger:
- d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2)
- d = √ ((3 - 4)2 + (3 - -1)2 + (0 - 12)2)
- d = √ ((- 1)2 + (4)2 + (-12)2)
- d = √ (1 + 16 + 144)
- d = √ (161)
- d = 12,69. Dette er radius af vores kugle.
- I vores eksempel ville vi plugge (4, -1, 12) til (x1, y1, z1) og (3, 3, 0) for (x2, y2, z2), løsningen som følger:
-
 4 Ved at i almindelige tilfælde r = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). I en kugle er hvert punkt på overfladen af kuglen den samme afstand fra midtpunktet. Hvis vi tager den tredimensionelle afstandsformel ovenfor og erstatter "d" -variablen med "r" -variablen for radius, får vi en form for ligningen, som kan finde radiusen, der er givet et centralt punkt (x1, y1, z1) og ethvert tilsvarende overfladepunkt (x2, y2, z2).
4 Ved at i almindelige tilfælde r = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). I en kugle er hvert punkt på overfladen af kuglen den samme afstand fra midtpunktet. Hvis vi tager den tredimensionelle afstandsformel ovenfor og erstatter "d" -variablen med "r" -variablen for radius, får vi en form for ligningen, som kan finde radiusen, der er givet et centralt punkt (x1, y1, z1) og ethvert tilsvarende overfladepunkt (x2, y2, z2). - Ved at kvadre begge sider af denne ligning får vi r2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2. Bemærk, at dette i det væsentlige er lig med grundsfære ækvationen r2 = x2 + y2 + z2 som antager et midtpunkt på (0,0,0).
 Minotauromaquia
Minotauromaquia
 1 Find radius, hvis du kender diameteren. Radien er halve diameteren, så brug formlen r = D / 2. Dette er identisk med metoden til beregning af en cirkels radius fra dens diameter.[1]
1 Find radius, hvis du kender diameteren. Radien er halve diameteren, så brug formlen r = D / 2. Dette er identisk med metoden til beregning af en cirkels radius fra dens diameter.[1]  2 Find radiusen, hvis du kender omkredsen. Brug formlen C / 2π. Da omkredsen er lig med πD, som er lig med 2πr, vil opdeling af omkredsen med 2π give radius.[2]
2 Find radiusen, hvis du kender omkredsen. Brug formlen C / 2π. Da omkredsen er lig med πD, som er lig med 2πr, vil opdeling af omkredsen med 2π give radius.[2] 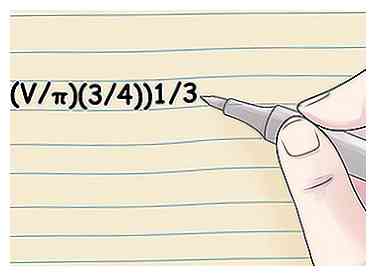 3 Beregn radius, hvis du kender en sfære. Brug formlen ((V / π) (3/4))1/3.[3] Volumenet af en kugle er afledt af ligningen V = (4/3) πr3. Løsning for r-variablen i denne ligning får ((V / π) (3/4))1/3 = r, hvilket betyder at radius af en kugle er lig med volumen divideret med π, gange 3/4, alt taget til 1/3 effekten (eller kubuskottet.)[4]
3 Beregn radius, hvis du kender en sfære. Brug formlen ((V / π) (3/4))1/3.[3] Volumenet af en kugle er afledt af ligningen V = (4/3) πr3. Løsning for r-variablen i denne ligning får ((V / π) (3/4))1/3 = r, hvilket betyder at radius af en kugle er lig med volumen divideret med π, gange 3/4, alt taget til 1/3 effekten (eller kubuskottet.)[4]  4 Find radius fra overfladeområdet. Brug formlen r = √ (A / (4π)). Overfladearealet af en kugle er afledt af ligningen A = 4πr2. Løsningen for r-variablen giver √ (A / (4π)) = r, hvilket betyder at en radius radius svarer til kvadratroten af overfladeområdet divideret med 4π. Du kan også tage (A / (4π)) til 1/2 strøm til det samme resultat.[5]
4 Find radius fra overfladeområdet. Brug formlen r = √ (A / (4π)). Overfladearealet af en kugle er afledt af ligningen A = 4πr2. Løsningen for r-variablen giver √ (A / (4π)) = r, hvilket betyder at en radius radius svarer til kvadratroten af overfladeområdet divideret med 4π. Du kan også tage (A / (4π)) til 1/2 strøm til det samme resultat.[5]  1 Identificer de grundlæggende målinger af en kugle. Radien (r) er afstanden fra det nøjagtige centrum af kuglen til ethvert punkt på kuglens overflade. Generelt kan du finde radius af en kugle, hvis du kender diameteren, omkredsen, lydstyrken eller overfladearealet.
1 Identificer de grundlæggende målinger af en kugle. Radien (r) er afstanden fra det nøjagtige centrum af kuglen til ethvert punkt på kuglens overflade. Generelt kan du finde radius af en kugle, hvis du kender diameteren, omkredsen, lydstyrken eller overfladearealet.  2 Brug forskellige målinger til at finde radius. Du kan bruge diameteren, omkredsen, volumenet og overfladeområdet til at beregne radius af en kugle. Du kan også beregne hvert af disse tal, hvis du kender længden af radiusen selv. For at finde radiusen, så prøv at vende formlerne til disse komponenters beregninger. Lær formlerne, der bruger radiusen for at finde diameter, omkreds, volumen og overfladeareal.
2 Brug forskellige målinger til at finde radius. Du kan bruge diameteren, omkredsen, volumenet og overfladeområdet til at beregne radius af en kugle. Du kan også beregne hvert af disse tal, hvis du kender længden af radiusen selv. For at finde radiusen, så prøv at vende formlerne til disse komponenters beregninger. Lær formlerne, der bruger radiusen for at finde diameter, omkreds, volumen og overfladeareal.  1 Find (x, y, z) koordinaterne for kuglens centrale punkt. En måde at tænke på radius af en kugle er som afstanden mellem punktet i centrum af kuglen og et hvilket som helst punkt på kuglens overflade. Fordi dette er sandt, hvis du kender punktets koordinater i centrum af kuglen og af ethvert punkt på overfladen, kan du finde kuglens radius ved blot at beregne afstanden mellem de to punkter med en variant af de grundlæggende afstand formel. For at begynde, find koordinaterne for kugles midtpunkt. Bemærk, at fordi kugler er tredimensionale, vil dette være et (x, y, z) punkt snarere end et (x, y) punkt.
1 Find (x, y, z) koordinaterne for kuglens centrale punkt. En måde at tænke på radius af en kugle er som afstanden mellem punktet i centrum af kuglen og et hvilket som helst punkt på kuglens overflade. Fordi dette er sandt, hvis du kender punktets koordinater i centrum af kuglen og af ethvert punkt på overfladen, kan du finde kuglens radius ved blot at beregne afstanden mellem de to punkter med en variant af de grundlæggende afstand formel. For at begynde, find koordinaterne for kugles midtpunkt. Bemærk, at fordi kugler er tredimensionale, vil dette være et (x, y, z) punkt snarere end et (x, y) punkt.  2 Find koordinaterne for et punkt på overfladen af kuglen. Dernæst skal du finde (x, y, z) koordinaterne for et punkt på overfladen af kuglen. Dette kan være nogen peg på overfladen af kuglen. Fordi punkterne på overfladen af en kugle er ækvivalente fra midten punkt pr. Definition, vil ethvert punkt arbejde for at bestemme radiusen.
2 Find koordinaterne for et punkt på overfladen af kuglen. Dernæst skal du finde (x, y, z) koordinaterne for et punkt på overfladen af kuglen. Dette kan være nogen peg på overfladen af kuglen. Fordi punkterne på overfladen af en kugle er ækvivalente fra midten punkt pr. Definition, vil ethvert punkt arbejde for at bestemme radiusen.  3 Find radius med formlen d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Nu hvor du kender midten af kuglen og et punkt på overfladen, vil beregningen af afstanden mellem de to finde radius. Brug den tredimensionelle afstandsformel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), hvor d er lig med afstand, (x1, y1, z1) er lig med koordinaterne for midtpunktet, og (x2, y2, z2) er lig med koordinaterne for punktet på overfladen for at finde afstanden mellem de to punkter.
3 Find radius med formlen d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Nu hvor du kender midten af kuglen og et punkt på overfladen, vil beregningen af afstanden mellem de to finde radius. Brug den tredimensionelle afstandsformel d = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2), hvor d er lig med afstand, (x1, y1, z1) er lig med koordinaterne for midtpunktet, og (x2, y2, z2) er lig med koordinaterne for punktet på overfladen for at finde afstanden mellem de to punkter.  4 Ved at i almindelige tilfælde r = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). I en kugle er hvert punkt på overfladen af kuglen den samme afstand fra midtpunktet. Hvis vi tager den tredimensionelle afstandsformel ovenfor og erstatter "d" -variablen med "r" -variablen for radius, får vi en form for ligningen, som kan finde radiusen, der er givet et centralt punkt (x1, y1, z1) og ethvert tilsvarende overfladepunkt (x2, y2, z2).
4 Ved at i almindelige tilfælde r = √ ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). I en kugle er hvert punkt på overfladen af kuglen den samme afstand fra midtpunktet. Hvis vi tager den tredimensionelle afstandsformel ovenfor og erstatter "d" -variablen med "r" -variablen for radius, får vi en form for ligningen, som kan finde radiusen, der er givet et centralt punkt (x1, y1, z1) og ethvert tilsvarende overfladepunkt (x2, y2, z2).